Research

Rooted America: Immobility and Segregation of the Intercounty Migration Network (American Sociological Review  2023)

Despite the popular narrative that the United States is a "land of mobility," the country may have become a "rooted America" after a decades-long decline in migration rates. This paper interrogates the lingering question about the social forces that limit migration, with the empirical focus on the internal migration in the United States. We propose a systemic, network model of migration flows, combining demographic, economic, political, geographical factors and network dependence structures that reflect the internal dynamics of migration systems. Using valued temporal exponential-family random graph models, we model the network of inter-county migration flows during the 2011-2015 period. Our analysis reveals a pattern of segmented immobility, where fewer people migrate between counties with dissimilar political contexts, levels of urbanization, and racial compositions. Probing our model using "knockout experiments" suggests that one would have observed approximately 4.6 million (27%) more inter-county migrants each year were the segmented immobility mechanisms inoperative. The paper offers a systemic view of internal migration and reveals the social and political cleavages that underlie geographical immobility in America.

California Exodus? A Network Model of Population Redistribution in the United States (Journal of Mathematical Sociology  2023)

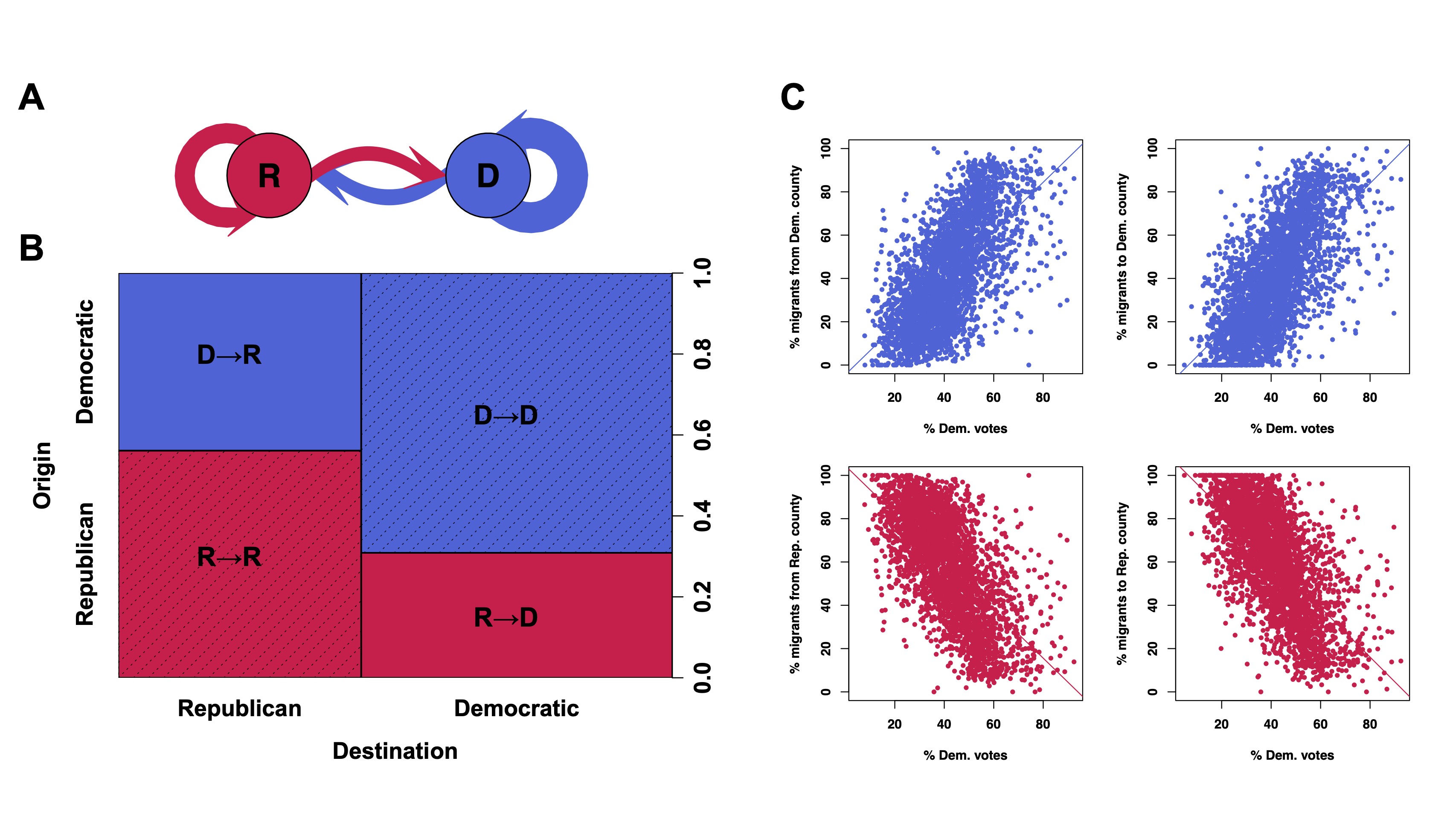
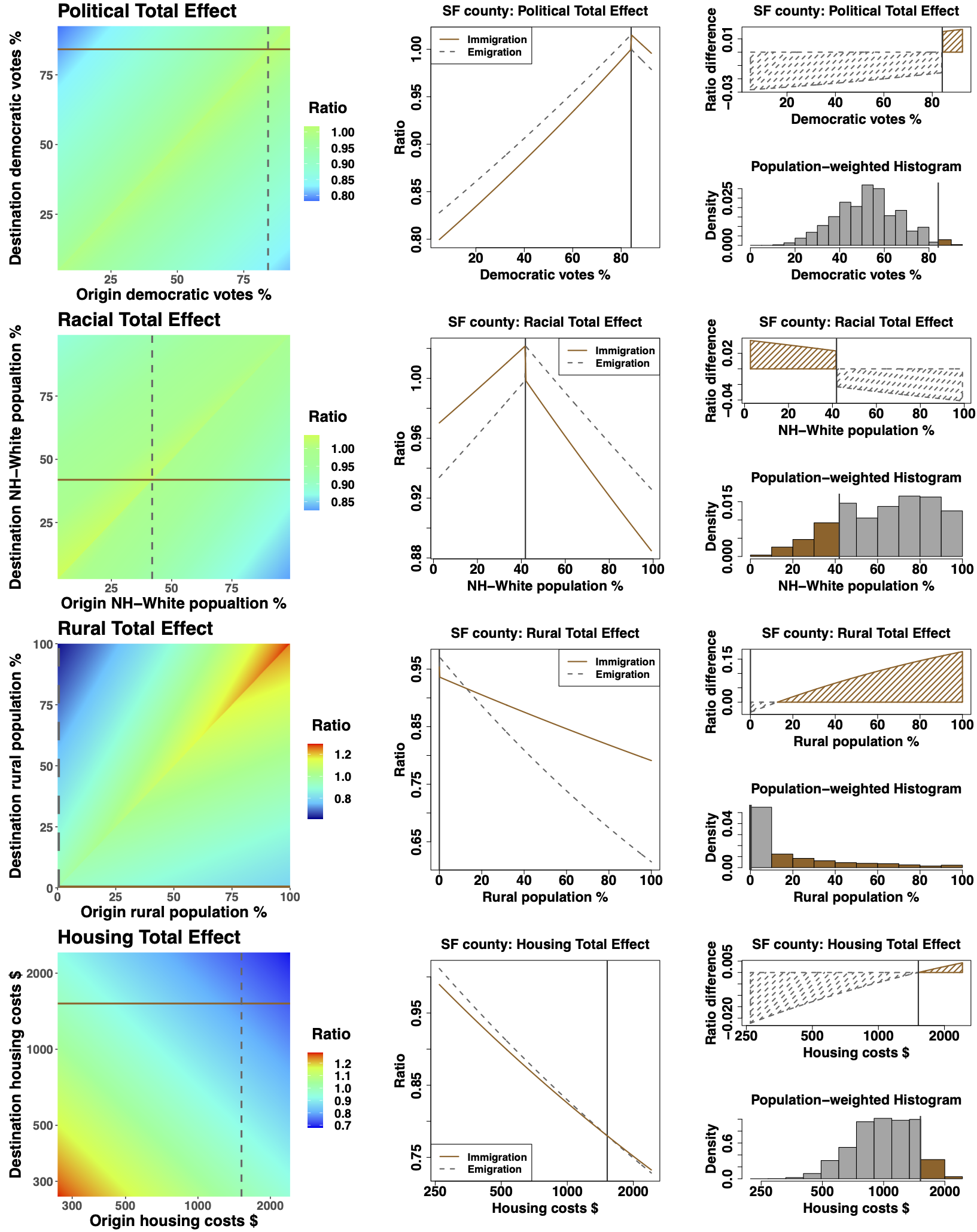
Motivated by debates about California's net migration loss, we employ valued exponential-family random graph models to analyze the inter-county migration flow networks in the United States. We introduce a protocol that visualizes the complex effects of potential underlying mechanisms, and perform knockout experiments to quantify their contribution to the California Exodus. We find that racial dynamics contribute to the California Exodus, urbanization ameliorates it, and political climate and housing costs have little impact. Moreover, the severity of the California Exodus depends on how one measures it, and California is not the state with the most substantial population loss. The paper demonstrates how generative statistical models can provide mechanistic insights beyond simple hypothesis-testing.

Parameter Estimation Procedures for Exponential-Family Random Graph Models on Count-Valued Networks: A Comparative Simulation Study (Social Networks  2024)

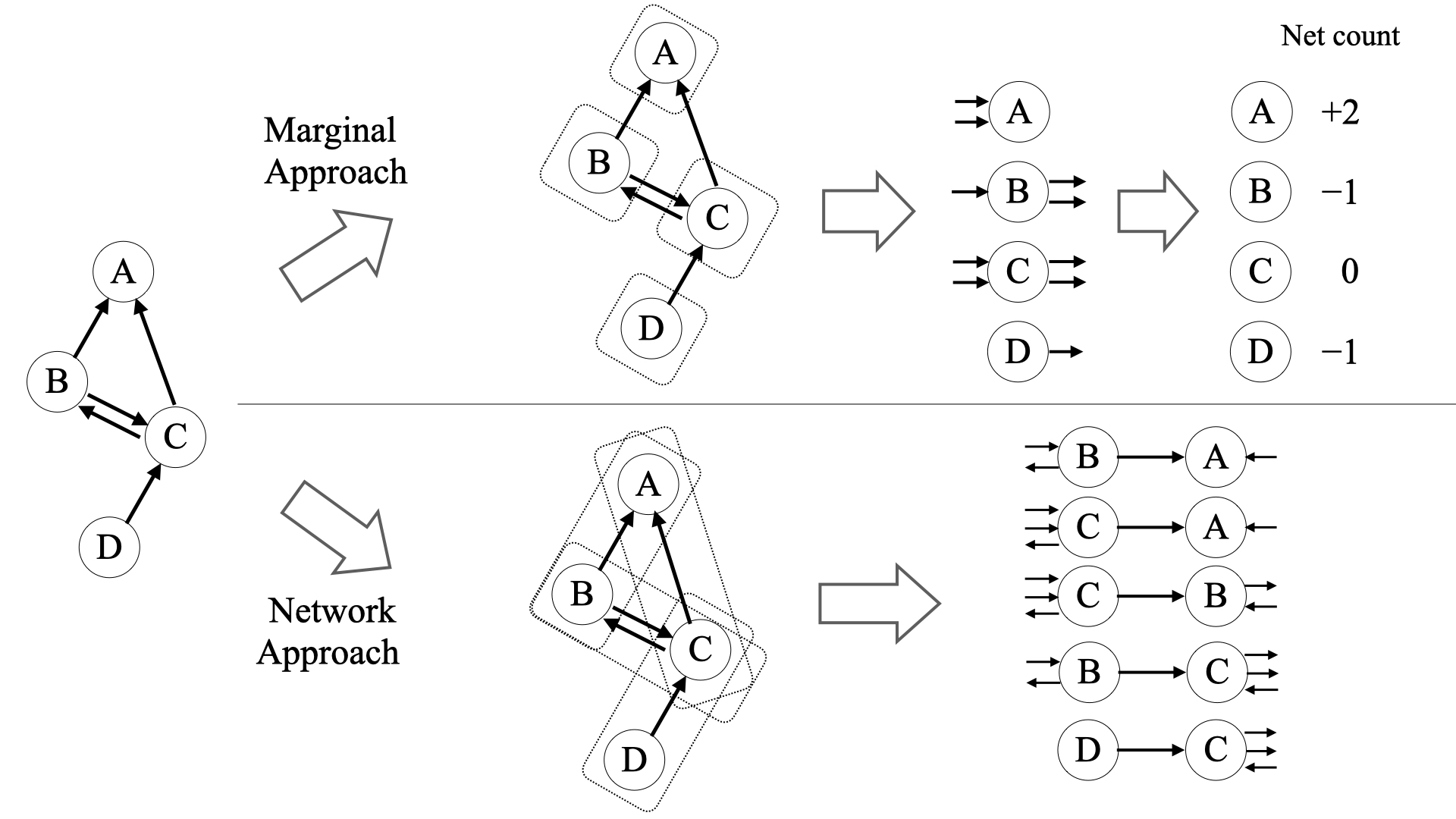
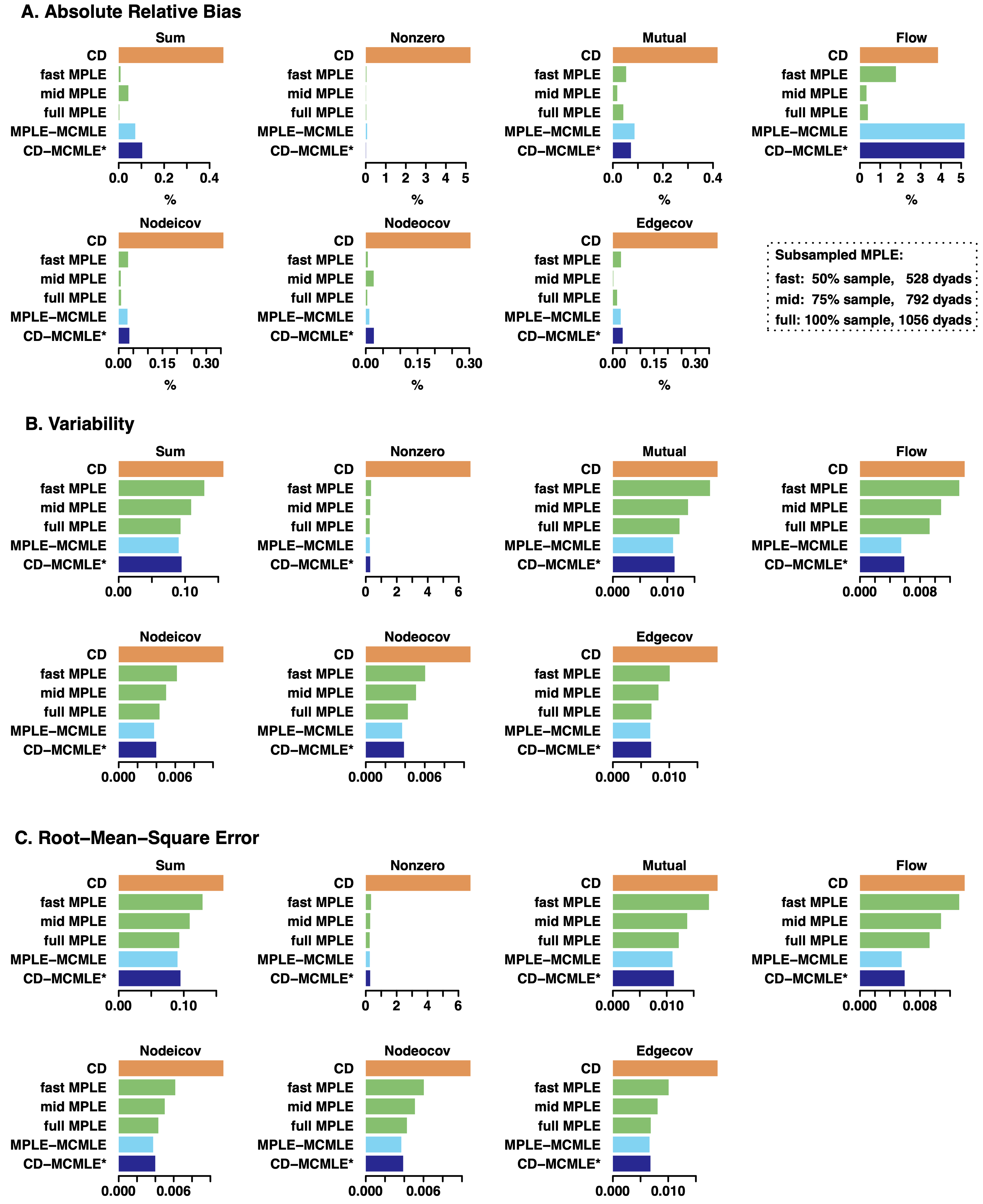
Computation remains a hurdle for analysis of valued networks using exponential-family random graph models (ERGMs). We implement an efficient parallelable subsampled Maximum Pseudo-Likelihood Estimation (MPLE) method. We then perform a comparative simulation study to evaluate estimation quality and speed of MPLE, Contrastive Divergence (CD), and Monte Carlo Maximum Likelihood Estimation (MCMLE). Results show that edge value variance is a key factor in method performance, while network size mainly influences their relative merits in computational time. The paper concludes with a guideline for choosing and tuning computational methods for valued ERGM estimation.

Marginal-preserving Imputation of Three-way Array Data in Nested Structures, with Application to Small Areal Units (Sociological Methodology  2024)

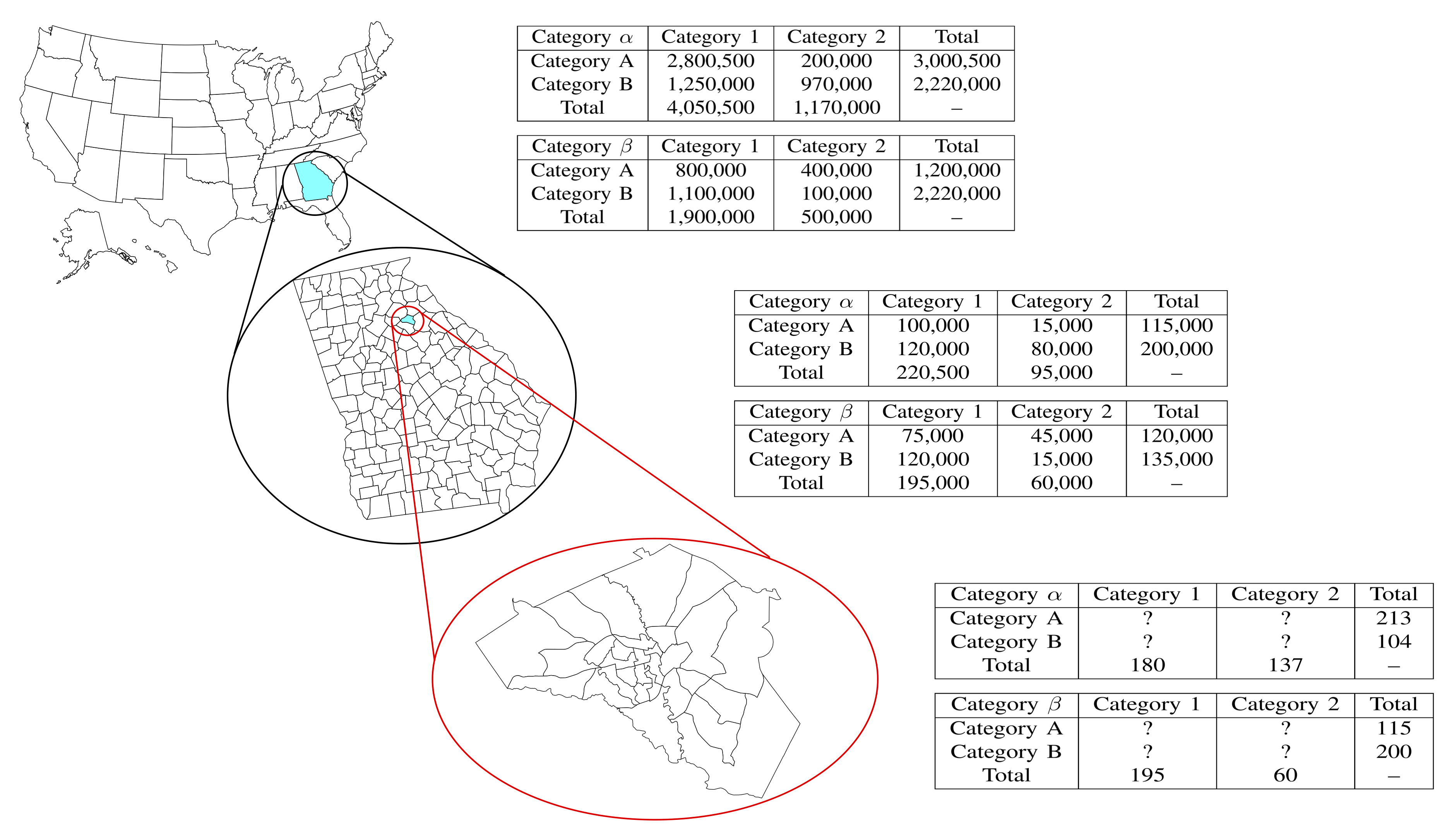
Geospatial population data is typically organized into nested hierarchies of areal units, in which each unit is a union of units at the next lower level. Despite increasing interest in analyses at fine geographical detail, these lowest rungs of the areal unit hierarchy are often incompletely tabulated due to cost, privacy, or other considerations. We introduce a novel algorithm to impute crosstabs of up to three dimensions (e.g., race, ethnicity, and sex) from marginal data combined with data at higher levels of aggregation. Our method exactly preserves the observed fine-grained marginals, while approximating higher-order correlations observed in more complete higher-level data. We show how this approach can be used with U.S. Census data via a case study involving differences in exposure to crime across demographic groups, showing that the imputation process introduces very little error into downstream analysis, while depicting social process at the more fine-grained level.

Geographical Patterns of Social Cohesion Drive Disparities in Early COVID Infection Hazard (PNAS  2022)

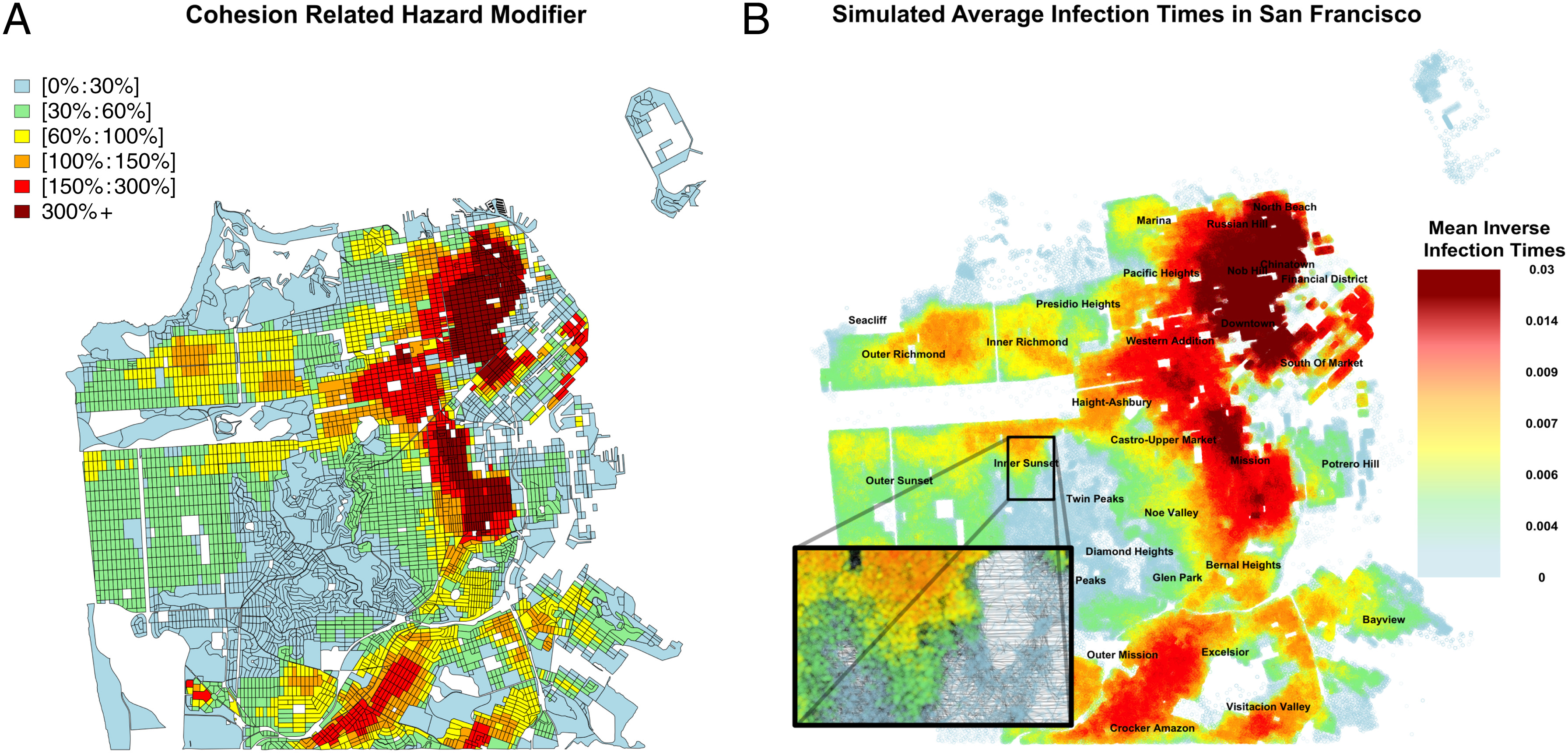
The uneven spread of COVID-19 has resulted in disparate experiences for marginalized populations in urban centers. Using computational models, we examine the effects of local cohesion on COVID-19 spread in social contact networks for the city of San Francisco, finding that more early COVID-19 infections occur in areas with strong local cohesion. This spatially correlated process tends to affect Black and Hispanic communities more than their Non-Hispanic White counterparts. Local social cohesion thus acts as a potential source of hidden risk for COVID-19 infection.

Spatial Heterogeneity Can Lead to Substantial Local Variations inCOVID-19 Timing and Severity (PNAS  2020)

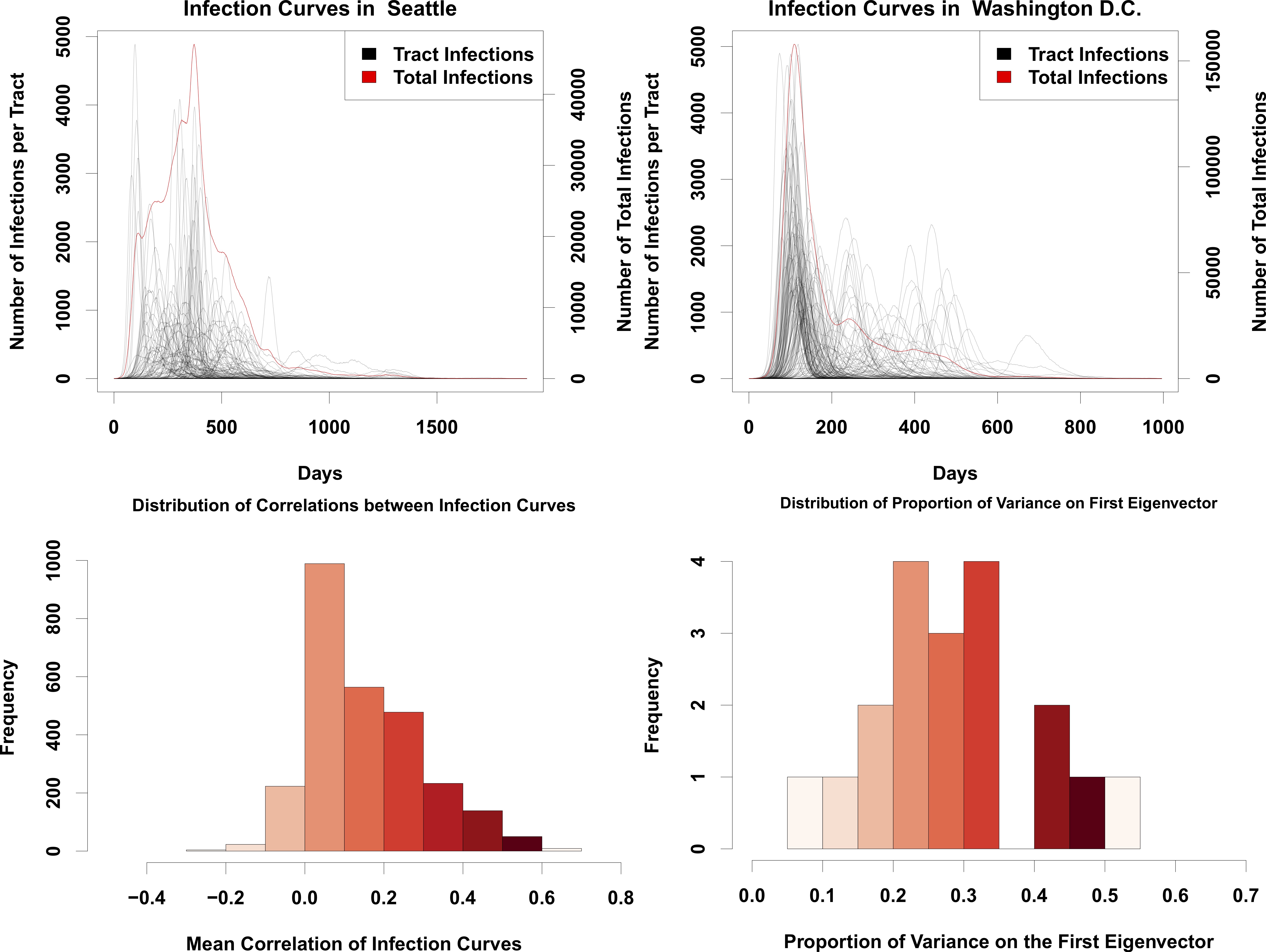
Standard epidemiological models for COVID-19 employ variants of compartment (SIR) models at local scales, implicitly assuming spatially uniform local mixing. Using a diffusion model based on interpersonal contact networks, this paper shows that the spread of COVID-19 has distinct timing and severity across different parts of a city. The paper demonstrates that spatial heterogeneity can produce dramatic differences in social exposures to those with the illness, and stress local healthcare systems differently in timing and extremity.